Binômio

 Binômio de Newton 

 O que é binômio?

Em matemática, binómio de Newton (na grafia portuguesa) ou binômio de Newton (na grafia brasileira) é uma fórmula que permite desenvolver sob a forma de polinómio qualquer potência de um binómio

Exemplos de desenvolvimento de binômios de Newton:

a) (a + b)²  =  a² + 2ab + b²
b) (a + b)³  =  a³ + 3 a²b + 3ab² + b³
c) (a + b)⁴  =  a⁴ + 4 a³b + 6 a²b² + 4ab³ + b⁴
d) (a + b)⁵  =  a⁵ + 5 a⁴b + 10 a³b² + 10 a²b³ + 5ab⁴ + b⁵

Observações:
1) o desenvolvimento do binômio (a + b)ⁿ é um polinômio.
2) o desenvolvimento de (a + b)ⁿ possui n + 1 termos .
3) os coeficientes dos termos eqüidistantes dos extremos , no desenvolvimento de 
(a + b)ⁿ são iguais .
4) a soma dos coeficientes de (a + b)ⁿ é igual a 2ⁿ .

Um termo genérico T_p+1 do desenvolvimento de (a+b)ⁿ , sendo p um número natural, é dado por :

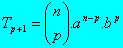
onde

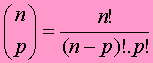
É denominado Número Binomial e C_n.p é o número de combinações simples de n elementos, agrupados p a p, ou seja, o número de combinações simples de n elementos de taxa p. 
Este número é também conhecido como Número Combinatório.

O Triângulo de Pascal

O seguinte triângulo é chamado triângulo de Pascal. Das inúmeras propriedades deste triângulo, destacamos que cada linha começa e acaba em 1 e adicionando dois números consecutivos de uma linha, obtemos o número colocado abaixo, na linha seguinte.

                                Exercícios Resolvidos:

  Calcular o 6º termo de (x-2y)⁸O termo geral é:

(⁸_k)(x)^8-k(-2y)^k = (⁸_k)(-2)^kx^8-ky^k

Se queremos o 6º termo, então k=5, logo o termo procurado é:

(⁸₅)(-2)⁵x³y⁵= 1792 x³y⁵

Determine o 7º termo do binômio (x + 2)⁷ , desenvolvido segundo as potências decrescentes de x.

Solução:

n=7;

p=6;

T_{p+1 =}C_{7,6 .}x^7-6.2⁶

 T_P+1=7x.6

T_p+1=448x

 Determine o termo médio do desenvolvimento do binômio (m/10+5b/m)⁸ .

Solução:

 T₅ =(8/4)(m/10)4.(5b/m)

T₅=70.m⁴/10000.625b⁴/m⁴

T₅=4375b⁴/1000=T₅=35b⁴/8

  No binômio (x³+1/y²)²⁵ escreva o termo que contém x⁹  calculando o respectivo coeficiente.

T_P+1=(25/p)(x³)^24-P(y^-2)^P                                   

T_P+1=(25/p)x^75-3Py^_2p 

     T₂₃=(25/22)x⁹y^-44  

     T₂₃=2300x⁹y^-44   

Determine o 7º termo do binômio (2x + 1)⁹ , desenvolvido segundo as potências decrescentes de x.

Solução:

Vamos aplicar a fórmula do termo geral de (a + b)ⁿ , onde a = 2x , b = 1 e n = 9. Como queremos o sétimo termo, fazemos p = 6 na fórmula do termo geral e efetuamos os cálculos indicados. Temos então:

T₇ =(9/6)! ===> 84;

T₇ =84.(2x)³.1⁶

T₇ = 84.8x³

T₇ =672x³

Portanto o sétimo termo procurado é 672x³

      ^{Exercícios propostos}

 1- Calcule o  6º termo no desenvolvimento de (a+3b)⁹

 R= T₆₌30618a⁴b⁵

2-Calcule o 11^º termo no desenvolvimento de(2x+3y)⁶

R= T_{4 ===>} 4320.x³y³ 

3-Calcular o termo médio no desenvolvimento de (2a+2/a)⁸

C_8,4= 70     * lembrete

R= T_5===> 17920

4- Qual é o termo em x⁵ no desenvolvimento de (x + 3)⁸ ?

T₄ = 1512.x⁵

5-Qual o termo médio do desenvolvimento de (2x + 3y)⁸

 R= 90720x⁴y⁴

 Att.

Pantoja